"Mějme člověka, kterého lze popsat jako směs bílého Karla a černého Andyho. Pokud se na něj podíváme pravým okem, neuvidíme směs, ale vždy buď Andyho nebo Karla. A určitá pravděpodobnost, že ho uvidíme jako Karla, bude i v případě, že se narodil jako Andy. Pokud se však na něj podíváme levým okem, uvidíme buď dlouhověkého Metuzaléma nebo krátce žijícího Jana. A v době, kdy se na tohoto podivného člověka dívat nebudeme, tak si nedokážeme představit, co vlastně je"
Podivnosti kvantového světa
Nedávno se na Oslovi diskutovalo rozhraní mezi kvantovou a klasickou fyzikou. Otázky spojené s filozofickou interpretací kvantové fyziky jsou velice náročné a stále otevřené. Je jich široká škála a některé z nich jsou spojeny s velmi zajímavou oblastí kvantové teleportace a kryptografie, ve které dochází hlavně v poslední době k velmi intenzivnímu rozvoji s příslibem velmi širokých aplikací. Díky pokroku v laserové technice, technologiích optických vláken i detekci jednotlivých fotonů se daří provádět kvantovou teleportaci na stále větší vzdálenosti. To mě inspirovalo k tomu, že by bylo zajímavé napsat pro Osla článek o těchto problémech. Musím však upozornit, že nejsem na filozofickou interpretaci kvantové fyziky expert a už vůbec ne na kvantovou teleportaci nebo kryptografii, i když jako jaderný fyzik se v praxi s kvantovou fyzikou a jejími důsledky setkávám skoro každodenně. Navíc je hodně problémů v této oblasti velmi těžké objasnit srozumitelně, zajímavě a zároveň korektně a správně. Proto berte tento článek spíše jako podnět k přemýšlení či diskuzi a reakci, která by objasnila případné nepřesnosti a chyby, kterých se dopustím. I na internetu je řada článků o této problematice. Každý autor ji osvětluje svým specifickým způsobem. Doufám, že i můj příspěvek bude pro některé čtenáře přínosem v jejich poznávání této oblasti.
Měřitelné a neměřitelné veličiny pro popis reality
Na začátek našich úvah je třeba zdůraznit, že každá vědecká teorie (model, hypotéza) slouží „pouze“ pro popis reality. Tedy není reálným světem, ale pouze jeho popisem. Tento fakt vystupuje zvláště do popředí u kvantové fyziky, kde vlnová funkce, kterou k popisu fyzikální reality používáme, není přímo měřitelnou fyzikální veličinou. To je velký rozdíl oproti klasické fyzice, která stav systému popisuje pomocí přímo měřitelných fyzikálních veličin. Budeme-li mít jednu částici, je její stav popsán v rámci klasické fyziky pomocí její polohy a hybnosti. Obě tyto veličiny můžeme přímo měřit. V rámci kvantové fyziky však stav systému, tedy i zmíněné jedné částice, popisuje zmíněná vlnová funkce, která přímo měřitelná není. Teprve pomocí této vlnové funkce můžeme určovat hodnoty měřitelných veličin. Velice často se však jedná pouze o pravděpodobnost, že v daném místě a čase naměříme dané hodnoty ze souboru možných hodnot příslušných měřitelných veličin. V konkrétním případě nelze říci, jaká hodnota měřitelné veličiny se naměří. Lze jen říci, jaké bude rozdělení pravděpodobnostní výskytu různých naměřených hodnot pro velký počet měření ve stejné situaci.
Některé z měřitelných veličin nemůžeme navíc naměřit současně s velmi vysokou přesností. To se týká právě třeba polohy a hybnosti částice. Jestliže určíme polohu s extrémní přesností, pak hybnost určíme extrémně nepřesně. Vztah mezi neurčitostmi v určení takto spojené dvojice veličin určuje tzv. Heisenbergův princip neurčitosti. Ten říká, že součin neurčitostí v měření takto svázaných veličin je větší než zhruba Planckova konstanta (přesněji Planckova konstanta dělena čtyřmi pí). Kromě zmíněné dvojice polohy a hybnosti se to týká například i dvojice energie a času.
Důležitým aspektem kvantového světa je i to, že měření z principiálního hlediska ovlivňuje zkoumaný objekt a jedná se o interakci makroskopického měřícího přístroje s mikroskopickým objektem. Při popisu výsledku měření dochází k tzv. kolapsu vlnové funkce. Tím je v kvantové fyzice popsán průběh výběru konkrétních hodnot různých měřitelných veličin ze všech možných souborů hodnot. Zároveň tak dojde k tomu, že objekt od okamžiku měření popisuje úplně nová vlnová funkce. A právě s touto oblastí jsou spojeny dvě hlavní otázky filozofické interpretace kvantové fyziky. První se týká podstaty reality, tedy otázky, co je realitou, kterou popisuje vlnová funkce. Druhá pak podstaty měření, což je otázka, na které úrovni v řetězci od mikroskopického objektu přes makroskopický měřící přístroj k pozorovateli dochází k rozhodnutí výsledku pozorování. Princip této otázky ozřejmuje i známý myšlenkový pokus se Schrődingerovou kočkou, ke kterému se ještě vrátíme.
Než se pustíme dále, ještě bych připomenul, že neurčenost stavu se pochopitelně netýká třeba jen polohy či hybnosti objektu (částice), ale i dalších jeho charakteristik. Připomenu třeba situaci, kterou jsme si popisovali v článku o oscilacích neutrin Pozorujeme tři různé typy neutrin - elektronové, mionové a tauonové. Vlnová funkce, která jednotlivé typy neutrin popisuje, není čistým stavem, ale směsí (terminologicky správněji superpozicí) tří jiných stavů (označme je jako neutrino jedna, dvě a tři). Jestliže někde vznikne například elektronové neutrino, lze je popsat vlnovou funkci, která je přesně danou kombinací stavů jedna, dvě a tři. Pokud budeme popisovat pohyb tohoto neutrina, bude se podíl jednotlivých stavů měnit. Což je proces oscilací neutrin, který jsme si popsali ve zmíněném článku. Jak moc se bude vlnová funkce lišit od vlnové funkce popisující elektronové neutrino, závisí na energii neutrina a vzdálenosti, kterou uletělo. Při pozorování nemůžeme vidět neutrina jedna, dvě či tři, ale pouze elektronové, mionové či tauonové. Změna vlnové funkce se tak projeví v tom, že s určitou pravděpodobností budeme pozorovat buď elektronové, mionové nebo taonové neutrino. Při popisu tohoto pozorování tak dochází k projekci vlnové funkce do jednoho ze tří pozorovatelných stavů, což je už zmíněný kolaps vlnové funkce.

S podobným jevem, který se týkal oscilací neutrálních mezonů K, jsme se setkali v článku o symetriích, který řešil problém, jak mimozemšťanům sdělit, že jsme s hmoty a ne antihmoty a která ruka je levá. V tomto případě se ukazuje, že v procesech probíhajících pomocí silné interakce pozorujeme neutrální K mezony jako K0 nebo anti-K0. Přičemž, pokud vznikne v interakci mezon Ko, jde o stav popsaný jako čistý. V jeho dalším vývoji dochází k oscilacím a stav je popsán jako směs stavu K0 a anti-K0. Při detekci pomocí silné interakce tak pozorujeme buď K0 nebo anti-K0 s pravděpodobnostmi, které závisí na vzdálenosti detektoru a energii mezonu. To je v případě, že pozorujeme neutrální mezon K při silné interakci. Pokud však pozorujeme vliv slabé interakce na neutrální mezony K, například jejich rozpad, projeví se míchání stavů K0 a anti-K0 v pozorování nových částic KL a KS. Tedy dvě částice, z nichž KL má dobu života o několik řádů delší než mezon KS. Souvisí to s tím, že v silných interakcích se zachovává fyzikální veličina, která se označuje jako podivnost a ve slabé interakci se zachovávat nemusí. Podrobněji je to vysvětleno ve zmiňovaném článku.
Pokusím se o analogii z makrosvěta, ale berte ji pochopitelně s rezervou. Mějme člověka, kterého lze popsat jako směs bílého Karla a černého Andyho. Pokud se na něj podíváme pravým okem, neuvidíme směs, ale vždy buď Andyho nebo Karla. A určitá pravděpodobnost, že ho uvidíme jako Karla, bude i v případě, že se narodil jako Andy. Pokud se však na něj podíváme levým okem, uvidíme buď dlouhověkého Metuzaléma nebo krátce žijícího Jana. A v době, kdy se na tohoto podivného člověka dívat nebudeme, tak si nedokážeme představit, co vlastně je. Je vidět, že z hlediska naší makroskopické zkušenosti je taková vlastnost kvantového světa až absurdní.
Lokální a nelokální popis
Další velmi důležitý rozdíl mezi klasickým a kvantovým popisem světa je rozpor mezi lokální klasickou fyzikou (speciální teorií relativity) a nelokální kvantovou fyzikou. Co se tím má na mysli. V klasické fyzice platí, že fyzikální procesy v daném místě a čase mohou být ovlivněny jen ději probíhajícími ve stejném čase a „nekonečně“ malém okolí. Znamená to, že se působení mezi objekty šíří postupně prostoročasem od jednoho objektu k druhému. Nemůže k němu dojít okamžitě nějakým mimoprostorovým způsobem. Není tedy možné okamžité a bezprostřední působení na dálku. Například, kdyby zmizelo najednou Slunce, Země by se teprve až po zhruba osmi minutách začala pohybovat jinak než po původní oběžné dráze. A teprve v této době by také zmizela záře Slunce z naší oblohy.
Na druhé straně kvantová fyzika je nelokální. Souvisí to i s tím, že v klasickém světě jsou objekty lokalizované a v kvantovém světě objekty lokalizované být nemusí a stírá se rozdíl mezi částicí a vlnou. Jak jsme už zmiňovali, vlnová funkce, která popisuje kvantové objekty tak může být rozprostřena po velmi rozsáhlém prostoru. Navíc může vzájemně svazovat řadu objektů, které se můžou nacházet i velice daleko od sebe. Tím je dáno, že mohou vznikat situace, které popisuje tzv. propletený stav, který si popíšeme v následující části. Při popisu pozorování dochází ke zmiňovanému kolapsu vlnové funkce a tedy výběru pozorovaných veličin. A to najednou ve všech místech prostoru. A tedy v jednom okamžiku se určují měřené hodnoty společně i u velmi vzdálených objektů.
Propletený stav a EPR paradox
Jak už bylo zdůrazněno, popisujeme v kvantové fyzice systém vlnovou funkcí, která není měřitelnou veličinou a teprve její kvadrát definuje pravděpodobnost, že změříme nějakou částici v daném stavu. Taková vlnová funkce popisuje systém komplexně v rozsáhlém prostoru. Můžeme tak mít dvě částice, jejichž stavy jsou vzájemně svázány (třeba nějakým zákonem zachování) a je třeba je popisovat společnou vlnovou funkcí.

Velmi často se v tomto případě uvažuje spin, což je kvantová veličina chovající se jako momentu hybnosti. Stejně jako v makrosvětě se musí i v kvantovém světě moment hybnosti a tedy i spin zachovávat. V makroskopickém světě je moment hybnosti vektorem, u kterého můžeme určit všechny jeho tři jeho složky. Jeho velikost může nabývat libovolné hodnoty. V kvantovém světě je tato veličina opět vektorem, ale lze současně měřit jen její velikost a pouze jednu složku (projekci spinu do jednoho směru). Navíc jsou jeho velikost i měřená složka kvantované. Elementárním kvantem spinu (momentu hybnosti) je známá Planckova konstanta. A v řadě předchozích článků jsem se zmiňoval o rozdílu mezi fermiony, jejichž hodnota spinu je poločíselným násobkem Planckovy konstanty, a bosony, jejichž hodnota spinu je celočíselným násobkem Planckovy konstanty.
Ale teď zpátky k propleteným kvantovým stavům. Nechť jsou vyzářeny dva elektrony. Ať je tato dvojice částic vyzářena s celkovým momentem hybnosti nulovým. Pak musíme díky zákonu zachování momentu hybnosti při libovolném pozorování tohoto systému vždy zjistit celkový moment hybnosti dvojice elektronů nulový. Elektron má velikost spinu polovinu Planckovy konstanty a může mít jen dvě projekce spinu vůči danému směru plus nebo mínus polovina Planckovy konstanty (jinak řečeno projekce nahoru nebo dolů). Pokud tedy naměříme projekci spinu do daného směru u jednoho elektronu kladnou, u druhého musíme ve stejném směru naměřit zápornou. Pro každý z dvojice elektronů není projekce spinu definována. Společná vlnová funkce je superpozicí dvou stavů. V prvním má první elektron projekci spinu kladnou a druhý zápornou a v druhém je tomu naopak. Kvadrát této vlnové funkce určuje pravděpodobnost, se kterou zjistíme konkrétní projekci u některého z nich. Jaký stav určíme v každém konkrétním měření u daného elektronu nelze říci. Když však změříme konkrétní projekci spinu u jedné částice, je pak stav druhé přesně a okamžitě definován, ať je v době měření jakkoliv daleko. Dochází k tomu už zmiňovanému kolapsu vlnové funkce.
V předchozím odstavci je popsána situace, která se označuje jako EPR paradox (paradox Einsteina, Podolského a Rosena). V daném případě v úpravě, kterou navrhl David Bohm. Albert Einstein, Boris Podolský a Nathan Rosen předpokládali lokálnost a argumentovali, že musí existovat nějaké „skryté“ parametry. Ty by měly již při vyzáření elektronů určovat, který z elektronů bude mít spin nahoru a který dolů. Jinak by se musela informace mezi objekty propleteného stavu přenášet nadsvětelnou rychlostí. Druhou možností, kterou obhajoval Niels Bohr, bylo smíření se s už zmíněnou nelokálností kvantové fyziky.
Lze nelokálnost kvantové fyziky potvrdit?
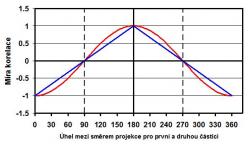
Rozhodnutí o tom, jestli existují skryté parametry, které sice nedokážeme pozorovat, ale definují naměřené veličiny už při vzniku stavu, nebo je kvantová fyzika nelokální, přinesl experiment navržený Johnem S. Bellem. Ten spočíval zase v měření projekce spinu dvojice elektronů do různých směrů pootočených o nějaký úhel ϑ. Podíváme se tedy na projekci spinu u prvního elektronu do nějakého směru a druhého elektronu na projekci do směru o zmíněný úhel pootočeného. Výsledek měření bude u obou elektronů vždy buď nahoru, nebo dolů. Pokud budou hodnoty projekce do daného směru u prvního elektronu i u druhého projekce do směru pootočeného o zmíněný úhel ϑ obě stejné (buď obě nahoru, nebo obě dolů), dostaneme korelaci a přiřadíme tomuto měření jedničku. Pokud budou opačné (dostaneme antikorelaci) přiřadíme mu mínus jedničku. Pokud změříme pro každý úhel spoustu případů a uděláme ze získaných sérií mínus a plus jedniček střední hodnotu, dostaneme v závislosti na úhlu ϑ různé hodnoty v intervalu mezi -1 až +1. O této veličině budeme mluvit jako o míře korelace pro dané nastavení směrů projekce spinů. Například pro ϑ = 0o dostaneme čistou hodnotu -1, jde o případ, který jsme popsali výše a pro který ze zákona zachování momentu hybnosti plyne, že projekce spinu jednotlivých elektronů musí být opačná a jde tedy o úplnou antikorelaci. Ze stejných důvodů bude úplná korelace a námi určovaná střední hodnota +1 pro úhel 180o. V případě, kdy je úhel 90o nebo 270o jsou vybrané směry projekce u jednotlivých elektronů na sebe kolmé. Protože lze vždy určit jen projekci spinu pouze do jednoho směru, nezávisí v tomto případě nijak výsledek měření u druhého elektronu na výsledku u prvního. Bude tak stejná pravděpodobnost dostat pro naši korelační veličinu hodnotu +1 i -1 a střední hodnota při velkém počtu měření, kdy dostaneme stejný počet plus i mínus jedniček, tak bude nula. Tomu bude stejně v případě platnosti nelokální kvantová teorie i v případě existence skrytých parametrů, které už na počátku definují, jak měření dopadnou. Ovšem pro úhly, které jsou mezi těmito hodnotami, to už bude jiné, tam se budou střední hodnoty námi sledované korelační veličiny v případě existence skrytých parametrů a nelokálnosti lišit. Střední hodnota sledované veličiny korelace bude v případě existence skrytých parametrů vždy mezi nulou a hodnotou na modré lomené křivce v obrázku. V případě platnosti nelokálnosti kvantového světa bude tato hodnota přesně dána červenou goniometrickou funkcí v obrázku. Je vidět, že pro dané úhly nemohou hodnoty míry korelace v případě lokálnosti a existence skrytých parametrů překročit určité meze. To je obsahem tzv. Bellových nerovností. Při správném nastavení experimentu je naměření větší absolutní hodnoty míry korelace důkazem, že opravdu platí nelokální kvantová teorie.
Při reálných experimentálních testech, zda jsou u propletených kvantových systémů splněny Bellových nerovností, se nejčastěji pracuje s fotony a jejich polarizací. Než se k nim dostaneme, budeme se v následujících pár odstavcích věnovat upřesněním některých pojmů souvisejících s polarizací zvláště elektromagnetického záření a fotonů. Pro další čtení není tato část nezbytně nutná. Pokud čtenář příslušné pojmy zná nebo bez dalšího vysvětlení příjme fakt, že jak světlo, tak i jednotlivý foton můžou být polarizovány, můžou „kmitat“ v některém směru kolmém na směr jejich šíření, tak lze následující část přeskočit.
Spin, helicita a polarizace fotonu
Význačným směrem, do kterého bude probíhat projekce spinu, může být směr pohybu příslušné částice. Orientace projekce spinu tak může být ve směru pohybu (hybnosti) dané částice nebo proti směru. V takovém případě mluvíme o helicitě. Její hodnota může být +1 v případě, že projekce spinu je orientována stejně jako směr pohybu (mluvíme také o pravotočivé helicitě) nebo -1 v případě, že projekce spinu je orientována opačně než směr pohybu (levotočivá helicita). Je třeba poznamenat, že helicita závisí na vzájemném pohybu pozorovatele a pozorované částice. Jestliže pozorujeme částici s pravotočivou helicitou (tedy +1) a posléze se začneme pohybovat ve směru pohybu tato částice rychleji než ona, tak se směr jejího pohybu vůči nám otočí, ale projekce spinu do směru zůstává stejná. Pravotočivá helicita částice se změní na levotočivou. Pochopitelně se v tomto případě změní levotočivá helicita částice na pravotočivou.
Řekli jsme si, že v případě spinu 1/2 jsou možné dvě projekce spinu a tedy dvě možné hodnoty helicity. V případě částice se spinem 1 jsou možné tři projekce spinu -1, 0 a +1. A také tři možné hodnoty helicity -1, 0, +1. Tato situace nastává například u deuteronu. V případě, že však částice má nulovou klidovou hmotnost, což je případ fotonu, jsou možné jen dvě projekce spinu do osy pohybu částice -1 a +1, tedy i jen dvě možné hodnoty helicity. U takových částic je ještě jedna specifická vlastnost, pohybují se rychlostí světla, takže pozorovatel nemůže zrychlit na rychlost větší. Helicita daného fotonu je tak pro každého pozorovatele stejná. Počet projekcí spinu NS s jeho rostoucí velikostí roste a lze je určit ze vztahu NS=2S+1, kde S je velikost spinu. U helicity už tomu tak není, Tam jsou stále dvě možné hodnoty v případě polocelého spinu a tři hodnoty pro celočíselný spin (dvě hodnoty v případě částic s nulovou klidovou hmotností).
Fotony jsou částicemi světla a helicita je na mikroskopické úrovni podstatou polarizace. Pro levotočivou či pravotočivou helicitu máme příslušnou kruhovou polarizaci. Eliptická či lineární polarizace se pak dostane příslušnou superpozicí levotočivé a pravotočivé kruhové polarizace. A tato superpozice popisuje jednotlivý foton s lineární polarizací. Popsané vlastnosti fotonů stojí i za makroskopickou polarizaci světla. V tomto případě jde o kmitání elektrického pole kolmo na směr pohybu světla, které udržuje stejný směr. Nepolarizované světlo kmitá také kolmo na směr pohybu světla ale do různých směrů. Pochopitelně můžeme dostat i pro makroskopické světlo kromě lineární i kruhovou či eliptickou polarizaci.
Výsledky experimentů testujících nelokálnost kvantové fyziky
První experimenty, které testovaly Bellovy nerovnosti, využívaly fotony s korelovanými polarizacemi vyzářenými ve vybrané kaskádě za sebou při následujících přechodech elektronů v obalu atomu vápníku. Proud atomů vápníku byl ozařován lasery a pomocí nich byly elektrony vybuzeny do daných stavů s vyšší energií. Přebytečné energie se atom zbavoval tak, že elektron nejdříve přeskočil do stavu s nižší energií. Přitom se vyzáří první foton. A z tohoto mezistavu téměř okamžitě přeskočí do základního stavu s vyzářením dalšího fotonu. Protože původní a vybuzený stav mají moment hybnosti nula a mezistav má nenulový moment hybnosti, klade zákon zachování momentu hybnosti jistá omezení na vztah polarizace jednotlivých fotonů ve vyzářené dvojici. Situace je tak velice podobná situaci dvojice elektronů, kterou jsme popisovali dříve. Dostáváme tak dvojici fotonů v propleteném stavu s korelovanými polarizacemi.
Pro zjišťování polarizace fotonů se využívaly i ve známé práci Alaina Aspecta v Orsay tzv. Wollastonovy polarizační hranoly složené ze dvou kusů islandského vápence. Ty vlastně určovaly směr projekce, podobně jako v dřívějším popisu propletené dvojice elektronů. Rozdíl je v tom, že v případě lineární polarizace definuje polarizace se směrem šíření světla rovinu. Při otočení polarimetru o 45o dostaneme nekorelované případy a při jeho otočení o 90o antikorelaci, při otočení polarimetru o 180o máme stejnou situaci jako na počátku. Pokud se podíváme na obrázek se zobrazením míry korelace na úhlu, který byl uveden v diskuzi elektronového páru, tak sice platí i pro případ studia Bellových nerovností pomocí polarizace fotonů. Ovšem úhel na ose x je v tomto případě dvojnásobkem úhlu mezi nastaveními dvou použitých polarizačních hranolů. V průběhu experimentu se dělalo vše pro to, aby nastavení polarizačního hranolu v jednom rameni (kam letěl první foton) neovlivňovalo situaci v druhém rameni, kam letěl ten druhý nebo dokonce proces vyzáření nějakou klasickou cestou. Proto se hranoly nastavovaly až po vyzáření fotonů. U těchto experimentů, které probíhaly na rozhraní sedmdesátých a osmdesátých let, byla vzdálenost mezi zdrojem fotonů v propleteném stavu a polarizačními hranoly šest metrů. Tuto vzdálenost uletí světlo za 20 ns. Výsledky měření se shodovaly s předpovědí nelokální kvantové mechaniky a vyloučily lokální teorii se skrytými parametry. Tím se prokázalo, že kvantový stav představuje úplný popis reality a že neurčitosti, které v popisu jsou, jsou objektivní a nejsou důsledkem našich neznalostí.

Později byla provedena řada stále přesnějších experimentů, kde se fotony v propleteném stavu posílaly na stále větší vzdálenost. Umožnil to hlavně rozvoj technologie laserů, optických vláken a detekce jednotlivých fotonů. Problém totiž je, že pracujeme právě s jednotlivými fotony a nelze použít zesilovače po trase. Nyní vzdálenosti, na které jsme schopni posílat fotony v propleteném stavu překonaly desítku kilometrů. Například v experimentu, který proběhl v roce 2008 v Ženevě, byla vzájemná vzdálenost dvojice fotonu v okamžiku měření 18 km. Takže zatímco celý proces měření trval pouhých 7 mikrosekund, na překonání vzdálenosti 18 km rychlostí světla je třeba 60 mikrosekund. A tedy „klasické“ ovlivnění signálem s rychlostí světla je nemožné. Pokrok v technologiích umožňuje přenést na velkou vzdálenost informaci o kvantovém stavu, který je superpozicí více stavů a dá se to využít v kvantové kryptografii.
Kvantová teleportace
Vlnovou funkci nelze měřit. Zajímavou otázkou tak je, zda a případně jak můžeme přenést informaci o kvantovém stavu, který je směsí různých stavů. Proces, který umožňuje přenést informaci o neurčitém kvantovém stavu na velkou vzdálenost, se označuje jako kvantová teleportace. Pomocí ní by si ve vzdáleném místě mohl někdo vytvořit systém ve stejném kvantovém stavu, jaký mám já. Potřebujeme k tomu vhodnou dvojici částic v kvantově propleteném stavu, který je přesně definován tzv. Bellův stav (propletené stavy musí být ortogonální). Jednu z nich si vezmu já a druhou vzdálený kolega. Buď si ji vezme před cestou, nebo mu ji musím nějak "klasicky" poslat. Pak provedu měření s tou mou provázanou částicí na stavu, který chce kolega u sebe replikovat. Tím dojde ke kolapsu vlnové funkce a vlnová funkce provázané částice se změní tak, že odráží stav, o kterém informaci potřebuji přenést. O výsledku měření musím kolegu informovat. A on už pak ví, jakou změnu se svou částicí musí provést, aby dostal přesně původní kvantový stav, který má replikovat. Zatím se kvantová teleportace provádí s fotony.
Jak je vidět, opravdu nejde o přenos informace o kvantovém stavu rychlostí větší než rychlost světla. Kolaps vlnové funkce sice proběhne díky nelokálnosti kvantové fyziky okamžitě, ale dokud nedostane vzdálený kolega informaci o mém výsledku měření, tak se díky kolapsu vlnové funkce provázaného stavu nic nedozví. Bez přenosu informace o výsledku měření na první částici (fotonu) klasickou cestou k tomu, kdo má druhou částici, jsou výsledky jeho měření pro něj náhodná. Takže kolaps vlnové funkce a nelokálnost kvantové fyziky nenarušuje kauzalitu a nelze je využít pro přenos informace rychlostí větší než je rychlost světla.
Než se přesuneme ke kvantové kryptografii, řekněme si ještě o jednom zajímavém příkladu s kvantovou teleportací na velké vzdálenosti. Zhruba před rokem se podařilo rakouským fyzikům transportovat propletený kvantový stav fotonů na vzdálenost 144 km z ostrova La Palma na ostrov Tenerife (jsou součástí Kanárských ostrovů). To bylo umožněno velmi výkonným zdrojem propletených dvojic fotonů s intenzitou okolo milionu za sekundu. Oba ve dvojici vzniklé fotony byly pomocí dvojitého optického systému vyslány směrem k observatoři s velkým optickým dalekohledem (patří organizaci ESA) na ostrově Tenerife.

Fotony, usměrněné tímto dalekohledem byly analyzovány a detekovány. Nejnáročnější byla identifikace propletených dvojic fotonů na velkém pozadí dalších fotonů. To se dařilo díky časové identifikaci, kdy časové okno pro fotony stejného páru bylo nastaveno na jednu nanosekundu. Díky měření korelací mezi polarizacemi fotonů ve dvojicích se podařilo prokázat, že během cesty se propletenost stavů nenarušila a lze provádět kvantovou teleportaci volným vzduchem i na takto velkou vzdálenost. Je to jeden s dalších kroků k využití kvantové teleportace v komunikaci s využitím družic. Místo experimentu bylo vybráno s ohledem na to, že jsou zde velmi dobré atmosférické podmínky. Je ovšem třeba zdůraznit, že i tak byl poměr mezi vyslanými a zachycenými dvojicemi fotonů deset milionů. Experiment tak zatím ještě pochopitelně neotvírá cestu ke kvantové komunikaci, ale je jedním s důležitých kroků. Blíže k reálné komunikaci mají právě již zmíněné experimenty na vzdálenosti v řádu pár desítek kilometrů, mezi které patří například nedávný experiment čínský.
Kvantová kryptografie
Když máme ověřeno, že opravdu dochází ke kolapsu vlnové funkce u kvantového stavu, můžeme to využít k vysílání kódovaných zpráv takovým způsobem, že bude snadné odhalit jejich případný „odposlech“. Kvantová fyzika nám pomáhá v kryptografii díky náhodnosti svých procesů. Umožňuje tak vytvářet velice efektivně plně náhodný šifrovací klíč. Jak ovšem dostat tento šifrovací klíč utajeně od příjemce k odesílateli? A právě kvantový stav umožňuje zařídit přenos tak, aby bylo možné zjistit odposlech. Je to dáno tím, že měření na kvantovém systému vede ke kolapsu vlnové funkce a systém se mění. Pokud tedy někdo provádí odposlech měřením na kvantovém systému dříve, lze to poznat.
V roce 1984 navrhli Charles Bennett a Gilles Brassard kryptografický protokol, který zmíněné vlastnosti kvantové fyziky využívá. Ze zřejmých důvodů se protokol označuje jako BB84 a pro jeho využití potřebujeme dva kanály. Jeden je klasický veřejný (telefon, internet) a bude přenášet zašifrovanou zprávu a několik vedlejších informací. Druhý kvantový slouží k domluvení tajného klíče. Ten by využíval polarizované fotony. Využívají se dvě dvojice polarizací, které jsou vzájemně kolmé. Byly už zmíněny v předchozím textu. Tedy třeba polarizace ve směru (rovině) nula a 90o je první dvojice navzájem kolmých polarizací. Druhá pak je ve směru 45o a 135o. Tyto dvojice (báze) jsou vzájemně nekorelované.
Popišme si příslušný protokol. Osoby, které v něm vystupují, se tradičně označují jako Alice, Bob a Eva. Alice a Bob si chtějí předat tajný klíč k dešifrování zprávy. Eva se snaží jej zjistit (odposlechnout), bez toho, aby se Bob s Alicí o tom dozvěděli. Alice generuje fotony náhodně polarizované do jedné ze čtyř zmíněných rovin tak, aby pravděpodobnost byla u každé z nich stejná. Bob nastavuje polarizační roviny polarimetru a měří polarizaci fotonů, přičemž náhodně střídá jednotlivé báze (dvojice kolmých polarizačních rovin). Zaznamenává výsledky měření, tedy polarizací jim měřených fotonů. Pokud vybral správnou bázi, dostane vždy signál nebo ne, podle toho, jaká byla polarizace fotonu vyslaného Alicí. Pokud zvolí špatnou bázi, dostane se stejnou pravděpodobností buď signál nebo ne. Vzpomeňte na míru korelace nula pro takové otočení polarizačních rovin. Alice pošle Bobovi veřejným kanálem pořadí, v jakém pořadí báze při vysílání vybírala. Konkrétní hodnoty polarizace si nechá pro sebe. Bob si zaznamená polarizace, které změřil u měření ve správné bázi. Tyto bity (nula je jedna polarizace, jednička polarizace kolmá) tvoří předávaný klíč. Ostatní měření, kde se Bob nestrefil do stejné báze, mohou být zapomenuty. Bob pak veřejným kanálem sdělí Alici, u kterého měření se strefil do správné báze. Alice i Bob tak znají jednotlivé bity klíče. Alice ví, jakou polarizaci vysílala a Bob ví, co naměřil. Potom se obětuje jistá část takto správně změřených hodnot, u kterých si Alice a Bob řeknou hodnoty polarizace, kterou Alice vyslala a Bob přijal. Pokud se shodují, nedochází k odposlechu a klíč lze použít k šifrování. Pokud by totiž Eva chtěla kvantový kanál odposlouchávat, musela by testovat polarizaci fotonu. Pokud se strefí do správné báze, dostane správný výsledek a polarizace fotonu se nezmění. Pokud se však strefí do špatné báze, změní se polarizace fotonu a Bob pak má poloviční šanci, že naměří špatný výsledek. Pokud Alice a Bob porovnají větší počet měření, mají téměř stoprocentní jistotu, že Evin odposlech zjistí. V takovém případě klíč zahodí a budou hledat spolehlivější kvantový kanál.

První pokusy s kvantovou kryptografií prováděl v roce 1989 již zmíněný Charles Benett a John A. Smolin. První zařízení mělo kvantový kanál dlouhý pouze 30 cm. Dnes se díky optickým vláknům a zlepšených zdrojů polarizovaných fotonů daří přenášet klíč pomocí kvantové kryptografie na vzdálenosti až kolem sta kilometrů. Rychlosti přenosu jsou zatím dost malé, ale i v této oblasti probíhá rychlý pokrok. Je dobrý důvod věřit, že pokrok laserové techniky, technologie optických vláken a detekční jednofotonové techniky (například polovodičových lavinových fotodiod) už relativně brzy umožní zavedení kvantové kryptografie do praxe.
Schrődingerova kočka
A teď se můžeme konečně dostat ke kvantové celebritě, která je živá nežívá či mrtvá nemrtvá snad v každém populárním povídání o kvantové fyzice. Souvisí s druhou hlavní otázkou kvantové fyziky zmíněnou na začátku. A to je otázka měření. Odlišnosti kvantové fyziky od naší makroskopické zkušenosti s měřením se nejvíce projevují ve světě mikroskopickém. Pozorování se uskutečňuje pomocí makroskopického přístroje, které vede v popisu ke kolapsu vlnové funkce kvantového systému. V původním myšlenkovém experimentu s Schrődingerovou kočkou máme neprůhlednou krabici a v ní je radioaktivní atom, zařízení se smrtícím plynem, které se spouští rozpadem toho atomu, a živou kočku. Když popisujeme kvantově příslušný proces, nedostaneme konkrétní čas rozpadu atomu, ale pouze pravděpodobnost, se kterou se po daném čase rozpadne. Proces rozpadu atomu je náhodný a daná je jen pravděpodobnost jeho průběhu za časovou jednotku. Vlnová funkce popisující rozpadající se atom je tak superpozicí stavu s atomem před rozpadem a po rozpadu. Pokud zahrneme do kvantového popisu i smrtící zařízení a kočku, tak budeme mít vlnovou funkci, která je superpozicí popisu kočky mrtvé a kočky živé. Kočka je však makroskopický objekt a pohled na ní, jak je současně živá i mrtvá je dost absurdní. Je tedy otázkou, co je vlastně realita, kterou reprezentuje kvantový stav popsaný superpozicí různých stavů a na které úrovni mezi kvantovým stavem a pozorovatelem dochází ke kolapsu vlnové funkce a co reálně se tím popisuje.
Existuje rozhraní mezi kvantovým a klasickým světem?
Právě to je důvodem k hledání mikroskopických systémů, které jsou v propleteném kvantovém stavu a svou hmotností se přesunují od klasických kvantových hodnot k hodnotám makroskopickým. Propletený kvantový systém dvou atomů yterbia se podařilo vytvořit v roce 2007. To byl sice velký krok k využití kvantové fyziky v počítačích, ale pořád máme mikroskopický objekt. Vytvoření co nejtěžšího objektu, který je popsán superpozicí více stavů a pozorování, zda a jak u něj probíhá kolaps vlnové funkce, je veden v řadě směrů. Některé z nich popsal nedávno Peter Kluvánek v článku na Oslovi. Jedná se například o pozorování interference při průchodu dvěma štěrbinami. Jde o opakování známého interferenčního experimentu s elektrony. Používají se stále těžší systémy, například Peterem Kluvánkem zmíněný experiment s molekulou fluorofulerénu, která má 100 atomů.

Jednou z cest je i zkoumání Boseho-Einsteinova kondenzátu, kdy máme atomy s celočíselným spinem, tedy bosony. Objekty s celočíseným spinem (bosony) se na rozdíl od objektů s poločíselným spinem (fermiony) mohou ve velkém množství nacházet v jednom kvantovém stavu. Boseho-Einsteinův kondenzát můžeme připravit ochlazením oblaku vhodných atomů na teploty velmi blízké absolutní nule. Tím se všechny atomy dostanou do jediného stavu s tou nejnižší energií. V jednom stavu jsou tak superponovány jeden boson přes druhý, vzájemně se nedají rozlišit a tvoří jeden obří superatom. Prvním atomem, u kterého se to podařilo, bylo rubidium. Později se vznik Boseho-Einsteinova kondenzátu pozoroval u řady dalších. V tomto případě už máme kvantový systém až s deseti tisícovkami atomů. Na velmi zajímavém projektu pracuje skupina QUANTUS, která studuje oblak atomů 87Rb ve stavu Boseho-Einsteinova kondenzátu v podmínkách mikrogravitace. Zatím testuje systém při volných pádech z výšky 146 m. Ale připravuje se pokračování těchto experimentů na oběžné dráze na stanici ISS. V tomto případě lze tento kvantový systém, který se chová jako jedna částice (superatom), použít pro interferometrii s „hmotnými“ vlnami (tedy opět obdoba experimentu se dvěma štěrbinani) a to s objektem o tisícovkách atomů. Kromě potvrzení kvantové superpozice by se v prostředí mikrogravitace pomocí této interferometrie dala provádět i velice přesná měření související s obecnou teorií relativity.
Je třeba zdůraznit, že není problém s tím, že by kvantová fyzika v limitních případech nepřecházela v klasickou fyziku, tedy s principem korespondence. Problém je s tím, jakou realitu popisuje superpozice různých stavů a co a na jaké úrovni se realizuje při kolapsu vlnové funkce. Jde o to, jak vypadá realita, když ji například ani principiálně pozorovat nemůžeme. Tedy například, co za realitu jsou třeba virtuální částice popisující interakce a řadu dalších kvantových procesů, které v hranicích daných Heisenbergovým principem neurčitosti mohou i „narušovat“ zákony zachování energie či hybnosti. V článku o těchto jevech souvisejících s popisem vakua jsem zmiňoval tři různé pohledy na průběh vzniku Hawkingova záření. Podstatné však je, že všechny při své aplikaci vedou při konkrétních výpočtech ke stejným hodnotám měřitelných veličin.
Závěr
Existuje několik filozofických interpretací popsaných kvantovaných vlastností. Žádný není úplně uspokojivý a všechny pochopitelně musí správně popisovat všechny známé měřitelné skutečnosti. Pokud se stejně jako v případě rozhodnutí mezi lokálností (se skrytými parametry) a nelokálností kvantové fyziky nenajde nějaký experiment, který by rozhodl mezi různými filozofickými interpretacemi, nelze mezi nimi najít tu správnou. Stejně jako v počátcích kvantové fyziky jsou otázky její filozofické interpretace stále otevřeny. Na druhé straně byla a je kvantová fyzika extrémně úspěšná v popisu (i když neúplném) našeho světa. Velká část fyziků se tak s touto situací, kdy Bůh s námi hraje kostky a občas dokonce tak, že na ně ani on sám nevidí, smířila. A zastává do značné míry pragmatický minimalistický pohled na kvantovou fyziku jako skvělého nástroje pro popis fyzikální reality.
Existuje řada článků o podivnostech kvantové fyziky. Dovolil bych si na závěr zmínit a doporučit velice pěknou a i laikům srozumitelnou sérii pěti článků v časopise Vesmír, kterou pod názvem „Kvantové hádanky“ napsali Miloslav Dušek a Pavel Cejnar.
Na hranici dvoch svetov Autor: Peter Kluvánek
Jak se vyznat ve všemožných částicích? Autor: Vladimír Wagner
Neutrina – jedny z nejlehčích a nejpodivuhodnějších částic Autor: Vladimír Wagner
Vypsat celou diskuzi
|
Jiří Brunner 03.01.2011 v 20:45 |
||
Odpovedět |
||
|
Můj názor Jan Schneider 11.07.2010 v 07:32 |
||
|
|
||
Odpovedět |
||
|
Díky všem diskutujícím. Vladimír Wagner 30.06.2010 v 21:34 |
||
|
S opravdovým potěšením jsem si přečetl diskuzi pod svým článkem. Je to jedna s dalších diskuzí na Oslovi, která je opravdu přínosem pro čtenáře. Moc bych si přál, aby právě takové diskuze zde převažovaly. Moc díky zvláště Pavlu Brožovi, kterého jsem četl se skutečným požitkem. A jeho styl, kterým dokáže podat náročnou věc velice srozumitelně a jasně i laikům, je mi inspirací. Ale jak už jsem psal, mé díky za velmi užitečné doplnění článku patří všem. |
||
Odpovedět |
||
| Děkuji autorovi za zajímavé téma, i diskutujícím Pavel Brož 01.07.2010 v 00:40 |
||
|
Mě se zase líbí, že máte odvahu napsat na osla článek, jehož téma je velice, velice nelehké přiblížit laikům. Vám se to opakovaně daří a já se vždycky těším na Vaše další články. Mně se to nedaří, mým prokletím je utápění se v detailech, nenašel bych odvahu pustit se do tak obtížného tématu. |
||
|
Dekuji a dodatek Petr Habala 30.06.2010 v 18:57 |
||
|
Vazeny pane Brozi; |
||
Odpovedět |
||
|
Okamžik pozorování Michal Podlesný 28.06.2010 v 13:02 |
||
|
Nelze vyřešit paradox Schr.kočky tím, že interakcí s vnějším světem a vlastně i okamžikem pozorování není otevření krabice, ale už detekce rozpadu atomu přístrojem se smrtícím plynem? Toto je makroskopický jev, ke kterému můžeme přiřadit i nějaký přenos informace z krabice ven. |
||
Odpovedět |
||
Frantisek Kriz 28.06.2010 v 16:22 |
||
|
V článku to nebylo zdůrazněno, ale krabice s kočkou musí být dokonale izolovaná, aby okamžikem pozorování výsledku bylo opravdu až její otevření. (Tento požadavek způsobuje, že se bude vždy jednat pouze o myšlenkový pokus). V souvislosti s tím bych se podivil nad článkem a diskuzí, proč nikdo nezmiňuje jev dekoherence? Je opravdu nepodstatný pro interpretace kvantové teorie? |
||
| Dekoherence problém měření neřeší Pavel Brož 29.06.2010 v 01:52 |
||
|
Abych vysvětlil proč dekoherence neřeší problém se Schrödingerovou kočkou, budu muset zabrousit trošinku více do matematiky – jak vím, Vám to nebude činit žádný problém, bohužel ale budeme muset obětovat porozumění u části čtenářů, kteří s tou matematikou nejsou až tak moc familiární. Nicméně bych rád začal pár terminologickými věcmi, které tu matematiku neobsahují, aby i ostatní čtenáři měli přibližnou představu, o čem se tady teď bavíme. |
||
František Kříž 29.06.2010 v 20:26 |
||
|
Za obsáhlé vysvětlení děkuji. Celé jsem to teda ještě nepromyslel ... Jenom abyste věděl že vaše úsilí nebylo zbytečné :) |
||
| Děkuji za reakci Pavel Brož 29.06.2010 v 23:18 |
||
|
Po pravdě řečeno máte můj obdiv, že mé nekonečné příspěvky vůbec čtete :-) |
||
|
Omluva Petr Habala 25.06.2010 v 10:35 |
||
|
Tohle melo byt u me otazky nize jako odpoved na reakci. Zase se mi to nepovedlo, omlouvam se. Navic jsem ten komentar vlozil az napotreti, poprve si to nevsimlo, ze jsem prihlasen, podruhe to vratilo dve stranky chybovych hlaseni. Nejak jsme si s timhle systemem nepadli do oka :-). |
||
Odpovedět |
||
|
No prave Petr Habala 25.06.2010 v 10:33 |
||
|
Jak vime, ze kocka je _opravdu_ ve vsech stavech? |
||
Odpovedět |
||
František Kříž 25.06.2010 v 22:01 |
||
|
Rozdíl mezi Schrodingerovou kočkou a Habalovým psem je principielně v tom, že náhodnost u kostky vyplývá čistě jen z naší neznalosti detailní informace o jejím pohybu a je tady "klasická". Narozdíl od času rozpadu atomu, který je dán kvantovou neurčitostí - a je neznámý i samotné přírodě. Jak to experimentálně rozlišit u těchto čtyřnožců mne zrovna nenapadá. Ale analogická otázka, jak rozlišit tyto dvě principiálně odlišné neznalosti v případě EPR experimentu odpověď má (viz ten graf "Závislost míry korelace na úhlu mezi směry, do kterých probíhá projekce spinu dvou částic ...") |
||
| Ono to má hlubší matematické kořeny Pavel Brož 26.06.2010 v 04:10 |
||
|
Důležité je to, že ta vlnová funkce popisující to kočku (nicméně každá vlnová funkce popisující jakýkoliv systém), má vývoj určený deterministickou Schrödingerovou rovnicí. Tzn. ten vývoj vlnové funkce je deterministický, a přirozeně vede k té superpozici té mrtvé a živé kočky. |
||
|
Metafyzika KM je experimentem nerozhodnutelná Pavel Brož 25.06.2010 v 00:59 |
||
|
Můžeme se pouze dohadovat, co je skutečné a co nikoliv, a co se vlastně s tou Schrödingerovou kočkou děje. Tuto věc nerozštípli za více než půlstoletí tisíce těch nejlepších odborníků. Tím nechci nijak znevažovat úvahy, které tady můžeme kolektivně rozvíjet, ale tento problém bude vyžadovat nějaký opravdu zásadní přelom v přístupu. Všechny aspoň trochu „normální“ vysvětlení plus hromady těch vyloženě ulítlých už byly vyzkoušeny, a všechny trpí zásadními charakteristickými neduhy. |
||
Odpovedět |
||
| Holograficka interpretacia ? Martin Chabada 25.06.2010 v 12:02 |
||
|
A co Bohmova "holograficka" interpretacia ? Realita "vznika" az okamihom pozorovania ako hologram tvoreny interferenciou vlnovej funkcie objektu a vlnovej funkcie "vedomia" (aj ked si nedokazem predstavit, co by to malo byt). Klasicke vlastnosti v makrosvete by mohli vyplyvat zo statistickehe "zosumarizovania realit" viacerych pozorovatelov. Podobne, ako makroskopicke zakony spravania plynov vyplyvaju z mikroskopickeho, statisticky spriemerovaneho, spravania molekul. |
||
| A přináší to něco nového? Pavel Brož 26.06.2010 v 02:04 |
||
|
Ono je důležité si uvědomit, že interpretace kvantové teorie jsou vlastně jenom takovou metafyzickou gymnastikou provozovanou jako jistý druh kratochvíle vědci, kteří mají zrovna potřebu se krátkodobě zabývat něčím filozofičtějším. Není to žádné téma, které by někoho uživilo. A ačkoliv se jej pro svou provokativnost zabývala už celá plejáda světoznámých fyziků včetně nositelů Nobelových cen, tak všichni tito výjimečně chytří lidé se proslavili na úplně jiných tématech, než jsou interpretace kvantové teorie. Pokud byste byl studentem fyziky a chtěl na toto téma dělat diplomku, těžko byste nejspíše sháněl školitele, a jako téma doktorské práce by to už byla téměř jistá profesní sebevražda. |
||
|
Tomas Bilka 23.06.2010 v 22:41 |
||
|
Jak jsem to pochopil ja (a netvrdim ze nutne spravne) z hlediska vnejsiho pozorovatele existuje realny stav v krabici jez je kombinaci stavu mrtva kocka a ziva kocka. Ten stav je neco co fyzikalne skutecne existuje. Cili neni to o tom ze v krabici je mrtva XOR ziva kocka a my jenom nevime co s ni je. V krabici je proste opravdu rozmazane cosi, co je zaroven zive i mrtve. |
||
Odpovedět |
||
| Re Roman Rodak 24.06.2010 v 11:18 |
||
|
myslim, ze to nejde takto jednoducho aplikovat aj na objekty makrosveta. dolezite je, ze vlnova funkcia skolabuje do urciteho stavu po prevedeni pozorovania. no a schroedingerova macka, tak ako kazda ina macka, ma urcite "samopozorovacie" schopnosti, ktore su v najzakladnejsej forme interakcie medzi atomami a v tej najkomplexnejsej forme je to pamat. Tym padom to ci macka zije je pre nu samotnu velmi dobre znamy fakt aj napriek tomu, ze vonkajsi pozorovatel nevie v akom je stave a podla mojho skromneho nazoru to nie je kvoli jej kvantovym vlastnostiam, ale jednoducho preto ze ju nevidi. Neviem si dost dobre predstavit macku, ktora by si po vytiahnuti z krabice pamatala sama seba ako mrtvozivu smuhu. |
||
Frantisek Kriz 24.06.2010 v 11:25 |
||
|
Je to v podstatě tak. Ale neřekl bych, že ten stav "reálně existuje", ale spíš existuje v našem matematickém popisu. Co "reálně existuje" nikdo uspokojivě nevymyslel. |
||
|
Dotaz na kocku Petr Habala 23.06.2010 v 19:58 |
||
|
Priznam se, ze nechapu poprask kolem S-kocky a proc na to potrebuji kvantovku. Pokud do krabice zavru kocku a chlapa s kostkou, ktery si kouli a po padnuti sestky kocku zardousi, pak mam naprosto stejnou situaci, neni-liz pravda? Dokud krabici neotevru, tak nevim, zda je ziva nebo mrtva. |
||
Odpovedět |
||
| Můj laický výklad Jakub Šenkýř 23.06.2010 v 22:48 |
||
|
Schroedingerova kočka má demonstrovat, jak šílené se zdají být vlastnosti kvantových částic v porovnání s nám známými makroskopickými objekty. Nejde o to, že dokud neprovedu měření (neotevřu krabici), nevím, v jakém stavu je zkoumaný objekt, ale že dokud neprovedu měření, je objekt ZÁROVEŇ ve všech možných stavech (s různou pravděpodobností). |
||
|
Autor píše: František Kříž 22.06.2010 v 00:59 |
||
|
"...s touto oblastí jsou spojeny dvě hlavní otázky filozofické interpretace kvantové fyziky. První se týká podstaty reality, tedy otázky, co je realitou, kterou popisuje vlnová funkce" |
||
Odpovedět |
||
| ad interpretace kvantové mechaniky Pavel Brož 22.06.2010 v 22:30 |
||
|
Bohužel žádná není falzifikovatelná experimentem. Pod pojmem interpretace kvantové mechaniky se myslí takové teoretické konstrukce, které jsou všechny ve shodě se všemi praktickými předpověďmi kvantově mechanického aparátu, byť k tomu používají naprosto nesrovnatelných metafyzických pojmů, jako je tomu třeba i v případě mnohasvětové interpretace Hugh Everetta. Zde jsou dva bližší odkazy, ten druhý je čemu také Everett věřil: |
||
František Kříž 22.06.2010 v 23:28 |
||
|
Za odpověď děkuji |
||
|
Kodaň Adolf Balík 21.06.2010 v 20:02 |
||
|
Každý statistik se učí, že nesmí věřit svým modelům. Že modely jsou tu od toho, abychom jich používali, ne abychom jim věřili. I samotné Popperovské pojetí vědy, které je vlastně opsáno z Fisherova pojetí statistiky, ve skutečnosti zastřeně říká to samé o jakékoliv teorii. Fyzici však zhusta trpí úchylkou víry ve své modely skoro jako teologové. Z toho vznikla dost ulítlá situace s pojetím standardní – tedy Kodaňské – interpretace kvantové teorie. Kvantová teorie je klasický statisticko fenomenologický model. Každý statistik by nad ním měl říci: Bacha nevěřit, změřit jen užitečnost. Je to statistika epifenoménu, lze tu čekat možnost vytvořit explanační model. |
||
Odpovedět |
||
Barak Obava 22.06.2010 v 14:21 |
||
|
Moc hezky jsi to vyexplanoval, Adolfe (tu by měl být blicí smajlík). |
||
|
Prechod medzi ... Martin Chabada 21.06.2010 v 17:37 |
||
|
... klasickym a kvantovym svetom je samozrejme plynuly, pretoze klasicky svet (a jeho zakony) je len statistickym sumarom (vzajomne nekoherentnych) hologramov. |
||
Odpovedět |
||
|
Nebojme se vlka nic... Tomáš Bartoň 21.06.2010 v 17:11 |
||
|
vždyť kvantovka je mladá nějakých sto let... bylo by divné kdyby soudobé meze určitelnosti nebyly někdy v budoucnu překonány... a vše se bude pak jevit velmi pravděpodobně hodně jinak :-) Ale každopádně - krásný článek...! |
||
Odpovedět |
||
|
Je to jednoduche ... Martin Chabada 21.06.2010 v 16:15 |
||
|
Realita je hologram vzniknuty interferenciou vlnovej funkcie vedomia pozorovatela a vlnovej funkcie danej castice/castic. |
||
Odpovedět |
||
| Bravo Jakub Šenkýř 21.06.2010 v 17:01 |
||
|
A tím je také rozřešena otázka, zda když v liduprázdném lese spadne strom, ozve se žuchnutí :-) |
||


